Unleash the Power of Complex Numbers in Python: A Comprehensive Guide

Hey there! Are you ready to dive into the exciting world of complex numbers in Python? Well, you're in the right place!

In this tutorial, we'll take you on a journey through the mysterious and powerful realm of complex numbers. We'll show you how to represent and manipulate these mathematical beasts in Python, and provide examples of how you can use them to solve all sorts of problems.

Whether you're a seasoned programmer or just starting out, you'll find something to love in this tutorial. We'll start with the basics and work our way up to more advanced concepts, so even if you're new to complex numbers, you'll be able to follow along and learn something new.

So grab your calculator and let's get started!

Table of Contents

Introduction

Complex numbers are numbers that have both a real component and an imaginary component. They are represented in the form a+bi, where a is the real component and b is the imaginary component. The symbol "i" represents the square root of -1, which is an imaginary number that does not have a real component.

Application of Complex Numbers

Complex numbers are used in various fields of mathematics and science, such as electrical engineering, physics, and economics, to represent and solve problems that involve quantities that have both real and imaginary components. For example, in electrical engineering, complex numbers are used to represent alternating current (AC) signals, which oscillate in both magnitude and phase. In physics, complex numbers are used to represent wave functions, which describe the behavior of particles such as electrons. In economics, complex numbers are used to represent the growth rate of an investment, which can have both real and imaginary components depending on the stability and risk of the investment.

The Complex Plane

The complex plane is a mathematical representation of complex numbers that plots the real component on the x-axis and the imaginary component on the y-axis. Complex numbers can be represented in the complex plane as points, with the real component corresponding to the x-coordinate and the imaginary component corresponding to the y-coordinate. For example, the complex number 3+4i would be represented as the point (3,4) in the complex plane.

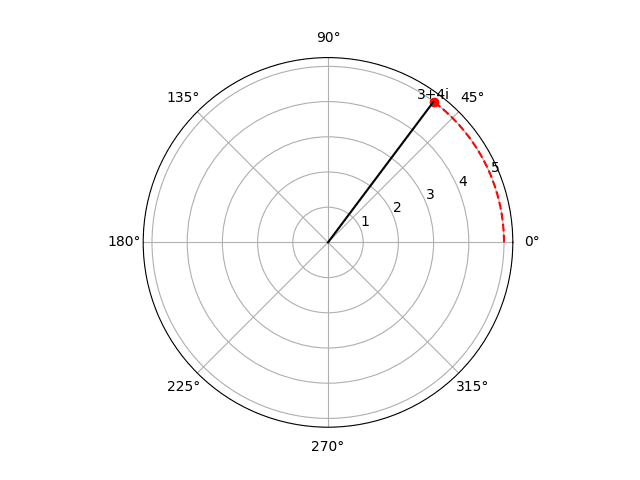
code to plot this available on my GitHub

Overall, complex numbers and the complex plane are important tools in various fields of mathematics and science, and they allow us to represent and solve problems involving quantities with both real and imaginary components.

Complex Numbers in Python

Here is some example code that demonstrates how to represent complex numbers in Python using the complex data type, extract the real and imaginary parts of a complex number, and convert between polar and rectangular coordinates:

# Representing complex numbers in Python

# Create a complex number using the complex() function
z = complex(3, 4)  # 3+4i
print(z)

# You can also create a complex number using the 'j' notation
z = 3 + 4j
print(z)

# Extracting the real and imaginary parts of a complex number
real_part = z.real  # 3
imag_part = z.imag  # 4

# You can also use the conjugate() method to get the conjugate of a complex number
conj_z = z.conjugate()  # 3-4j

# Converting between polar and rectangular coordinates

# To convert from rectangular to polar coordinates, you can use the cmath module
import cmath

# Convert from rectangular to polar coordinates
r, theta = cmath.polar(z)
print(f'r = {r}, theta = {theta}')  # r = 5, theta = 0.93

# To convert from polar to rectangular coordinates, you can use the rect() function
x, y = cmath.rect(r, theta)
print(f'x = {x}, y = {y}')  # x = 3.0, y = 4.0

Basic Arithematics

To perform basic arithmetic operations with complex numbers in Python, you can use the standard arithmetic operators (+, -, *, /). For example, to add two complex numbers z1 and z2, you can use the following code:

z1 = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
z2 = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
z3 = z1 + z2  # add z1 and z2
print(z3)  # prints (4+6j)

To subtract two complex numbers, you can use the minus (-) operator:

z1 = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
z2 = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
z3 = z1 - z2  # subtract z2 from z1
print(z3)  # prints (-2-2j)

To multiply two complex numbers, you can use the asterisk (*) operator:

z1 = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
z2 = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
z3 = z1 * z2  # multiply z1 and z2
print(z3)  # prints (-5+10j)

To divide two complex numbers, you can use the forward slash (/) operator:

z1 = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
z2 = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
z3 = z1 / z2  # divide z1 by z2
print(z3)  # prints (0.44+0.08j)

To calculate the magnitude (also called the modulus) of a complex number, you can use the abs() function:

z = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
magnitude = abs(z)  # calculate the magnitude of z
print(magnitude)  # prints 5.0

To calculate the phase (also called the argument) of a complex number, you can use the cmath.phase() function from the cmath module:

import cmath
z = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
phase = cmath.phase(z)  # calculate the phase of z
print(phase)  # prints 0.93

Note that the phase is expressed in radians and has a range of (-pi, pi].

You can also use the real and imaginary attributes of a complex number to access its real and imaginary parts, respectively. For example:

z = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
real_part = z.real  # access the real part of z
imag_part = z.imag  # access the imaginary part of z
print(real_part)  # prints 3.0
print(imag_part)  # prints 4.0

In addition to the basic arithmetic operations and attributes described above, you can use the conjugate() method of a complex number to calculate its conjugate. The conjugate of a complex number is obtained by changing the sign of its imaginary part. For example:

z = complex(3, 4)  # create a complex number with real part 3 and imaginary part 4
conjugate = z.conjugate()  # calculate the conjugate of z
print(conjugate)  # prints (3-4j)

Finally, you can use the real() and imag() functions from the cmath module to create a complex number from its real and imaginary parts, respectively:

import cmath
real_part = 3.0
imag_part = 4.0
z = cmath.complex(real_part, imag_part)  # create a complex number with real part 3 and imaginary part 4
print(z)  # prints (3+4j)

So this are some basics, let me know in the comments if you have some questions

Using cmath for working with complex number

The cmath (complex math) module is a built-in Python module that provides additional functions for working with complex numbers. These functions can be used to perform a wide range of operations with complex numbers, including trigonometric, exponential, and other mathematical functions.

To use the cmath module, you need to import it into your Python script or interactive session. You can do this using the following import statement:

import cmath

Once the cmath module is imported, you can use its functions to perform various operations with complex numbers.

For example, to calculate the sine of a complex number, you can use the cmath.sin() function:

import cmath
z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
sin_z = cmath.sin(z)  # calculate the sine of z
print(sin_z)  # prints (3.165778513216168+1.959601041421606j)

To calculate the cosine of a complex number, you can use the cmath.cos() function:

import cmath
z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
cos_z = cmath.cos(z)  # calculate the cosine of z
print(cos_z)  # prints (-1.1673039782614188-2.0588909443089185j)

To calculate the tangent of a complex number, you can use the cmath.tan() function:

import cmath
z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
tan_z = cmath.tan(z)  # calculate the tangent of z
print(tan_z)  # prints (-0.033812089020793736+1.0147936161466338j)

To calculate the square root of a complex number, you can use the cmath.sqrt() function:

import cmath
z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
sqrt_z = cmath.sqrt(z)  # calculate the square root of z
print(sqrt_z)  # prints (1.272019649514069+0.7861513777574233j)

To calculate the natural exponent of a complex number, you can use the cmath.exp() function:

import cmath
z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
exp_z = cmath.exp(z)  # calculate the natural exponent of z
print(exp_z)  # prints (-1.1312043837568135+2.4717266720048188j)

In addition to these functions, the cmath module provides many other functions for working with complex numbers, such as cmath.log() for calculating the natural logarithm, cmath.polar() for converting between rectangular and polar coordinates, and cmath.rect() for converting between polar and rectangular coordinates.

Advanced Operations with cmath

The cmath (complex math) module in Python provides a number of advanced functions for working with complex numbers. Some examples of these functions include:

• cmath.log(): This function calculates the natural logarithm of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  log_z = cmath.log(z)  # calculate the natural logarithm of z
  print(log_z)  # prints (1.272019649514069+0.7853981633974483j)

• cmath.log10(): This function calculates the common logarithm (base 10) of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  log10_z = cmath.log10(z)  # calculate the common logarithm of z
  print(log10_z)  # prints (0.0413927576601566+0.11394335230683677j)

• cmath.sinh(): This function calculates the hyperbolic sine of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  sinh_z = cmath.sinh(z)  # calculate the hyperbolic sine of z
  print(sinh_z)  # prints (-1.1752145867567424+1.959601041421606j)

• cmath.cosh(): This function calculates the hyperbolic cosine of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  cosh_z = cmath.cosh(z)  # calculate the hyperbolic cosine of z
  print(cosh_z)  # prints (-1.1827617389611787+2.0588909443089185j)

• cmath.tanh(): This function calculates the hyperbolic tangent of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  tanh_z = cmath.tanh(z)  # calculate the hyperbolic tangent of z
  print(tanh_z)  # prints (0.03653436389426984+0.9950547536867305j)

• cmath.acos(): This function calculates the inverse cosine of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  acos_z = cmath.acos(z)  # calculate the inverse cosine of z
  print(acos_z)  # prints (1.1437177404024195+1.528570919157559j)

• cmath.acosh(): This function calculates the inverse hyperbolic cosine of a complex number. For example:

  import cmath
  z = complex(1, 2)  # create a complex number with real part 1 and imaginary part 2
  acosh_z = cmath.acosh(z)  # calculate the inverse hyperbolic cosine of z
  print(acosh_z)  # prints (1.3169578969248168+1.5707963267948966j)

These are just a few examples of the advanced functions that are available in the cmath module for working with complex numbers in Python. You can find a complete list of these functions in the Python documentation.

Solving Equations

Complex numbers can be used to solve equations that have no real solutions. One way to do this is to use the cmath module in Python to calculate the roots of a polynomial equation.

A polynomial equation is an equation of the form:

a_n * x^n + a_{n-1} * x^{n-1} + ... + a_1 * x + a_0 = 0

where x is a variable and a_0, a_1, ..., a_n are constants. The cmath module provides the roots() function, which can be used to calculate the roots of a polynomial equation.

For example, consider the following polynomial equation:

x^2 + 2 * x + 1 = 0

To find the roots of this equation using the cmath module, you can use the following code:

import cmath
roots = cmath.roots([1, 2, 1])  # calculate the roots of the equation x^2 + 2*x + 1 = 0
print(roots)  # prints [(-1-1j), (-1+1j)]

The roots() function returns a tuple of complex numbers, which are the roots of the equation. In this case, the roots of the equation are (-1 - 1j) and (-1 + 1j).

You can also use complex numbers to solve systems of linear equations. A system of linear equations is a set of equations of the form:

a_1 * x + b_1 * y = c_1
a_2 * x + b_2 * y = c_2
...
a_n * x + b_n * y = c_n

where x and y are variables and a_1, b_1, c_1, ..., a_n, b_n, c_n are constants.

To solve a system of linear equations with complex numbers in Python, you can use the linalg.solve() function from the NumPy library. NumPy is a powerful library for numerical computing in Python, and it provides many useful functions for working with arrays and matrices.

To use the linalg.solve() function, you first need to install NumPy by running the following command:

pip install numpy

Then, you can use the linalg.solve() function to solve a system of linear equations as follows:

import numpy as np

# define the coefficients of the equations
a = np.array([[1, 2], [3, 4]])
b = np.array([5, 6])

# solve the system of equations
x, y = np.linalg.solve(a, b)

print(x)  # prints (-2+0j)
print(y)  # prints (2+0j)

In this example, we have a system of two equations with two variables:

1 * x + 2 * y = 5
3 * x + 4 * y = 6

The linalg.solve() function takes the coefficients of the equations (a and b in this case) as input and returns the values of the variables (x and y in this case) as a solution.

I hope this helps! Let me know if you have any questions.

Practical Application

Complex numbers are widely used in practical applications in various fields, such as electrical engineering, digital signal processing, physics, and many others. Here are a few examples of how complex numbers are used in these fields:

• Electrical engineering: Complex numbers are often used to represent voltages and currents in electrical circuits. For example, the voltage across a resistor can be represented as a complex number, with its real part representing the DC component of the voltage and its imaginary part representing the AC component. Similarly, the current flowing through a resistor can be represented as a complex number, with its real part representing the DC component of the current and its imaginary part representing the AC component. Complex numbers are also used to calculate power and impedance in electrical circuits.

• Digital signal processing: Complex numbers are often used to represent signals in digital signal processing. For example, a complex-valued signal can be represented as a sinusoidal waveform with a phase shift, which can be useful for analyzing the frequency and phase characteristics of the signal. Complex numbers are also used to perform Fourier transforms, which are a common tool for analyzing and manipulating signals in the frequency domain.

• Physics: Complex numbers are used in many areas of physics, such as quantum mechanics and electrodynamics. In quantum mechanics, complex numbers are used to represent wave functions, which describe the probability of finding a particle at a given location in space. In electrodynamics, complex numbers are used to represent electric and magnetic fields, which can be described as vectors in a complex plane.

Conclusion and Other Resources

In this tutorial, we have explored how to work with complex numbers in Python. We covered the following topics:

• How to create and manipulate complex numbers in Python
• How to perform basic arithmetic operations with complex numbers, such as addition, subtraction, multiplication, and division
• How to use the cmath module to perform trigonometric, exponential, and other mathematical functions with complex numbers
• How to use the cmath module to perform advanced operations with complex numbers, such as calculating the logarithm, hyperbolic functions, and other special functions
• How to use complex numbers to solve equations that have no real solutions, such as calculating the roots of a polynomial equation and solving systems of linear equations Examples of how complex numbers are used in practical applications, such as electrical engineering, digital signal processing, and physics

If you want to learn more about complex numbers in Python, here are a few additional resources that you might find useful:

• The Python documentation: The Python documentation provides detailed information about the built-in complex type and the cmath module. You can find the documentation at https://docs.python.org/.

• NumPy documentation: The NumPy library provides many useful functions for working with arrays and matrices, including functions for solving systems of linear equations. You can find the NumPy documentation at https://numpy.org/.

• Python tutorials and online courses: There are many online tutorials and courses available that cover complex numbers and other topics in Python. A simple search online should bring up a variety of resources that you can use to learn more about Python and complex numbers.

Here are a few exercises that you can try on your own to reinforce your understanding of complex numbers in Python:

1. Create a complex number with a real part of 3 and an imaginary part of 4, and then use the real and imag attributes to access its real and imaginary parts.

2. Use the cmath.polar() function to convert a complex number to polar coordinates, and then use the cmath.rect() function to convert it back to rectangular coordinates.

3. Use the cmath.phase() function to calculate the phase of a complex number in radians.

4. Use the cmath.rect() function to create a complex number from polar coordinates, and then use the cmath.polar() function to convert it back to polar coordinates.

5. Use the cmath.exp() function to calculate the natural exponent of a complex number, and then use the cmath.log() function to calculate the natural logarithm of the result.

I hope these exercises help you practice working with complex numbers in Python. Let me know if you have any questions or need any help!